모델의 속도를 높일 수 있는 최적화 알고리즘(Optimization Algorithms)을 알아보자.
1. Mini-Batch
지금까지 우리는 전체 데이터 X (\(n_x \times m\))에 대해 gradient를 계산하는 Batch gradient descent 방법을 사용했다.
Batch gradient descent는 m이 커질수록 gradient를 계산이 느려지는 문제가 있다.
전체 데이터를 mini-batch로 나눈뒤 gradient를 계산하는 Mini-Batch gradient descent 를 사용하여 gradient 계산 속도를 높일 수 있다.
ex) m=5,000,000인 데이터 셋을 mini-batch size=1,000으로 나누는 경우,
\(X^{\{1\}}, X^{\{2\}}, ... , X^{\{5,000\}}\) (\(n_x \times 1,000\))
\(Y^{\{1\}}, Y^{\{2\}}, ... , Y^{\{5,000\}}\) (\(1 \times 1,000\))
의 mini-batch로 나뉠 것이다.
Mini-Batch gradient descent는 각 mini-batch t(\(X^{\{t\}}, Y^{\{t\}}\))에 대해 gradient descent를 수행한다.
하나의 mini-batch에 대한 gradient descent를 1 epoch이라고 한다. 5,000개의 mini-batch의 경우 1 iteration에서 5,000 epoch을 진행한다.
하나의 데이터 \(x^{(t)}\)를 하나의 mini-batch \(X^{\{t\}}\)로 두는 경우 Stochastic gradient descent라고 한다. (mini-batch size=1)
Stochastic gradient descent은 noise가 많이 발생하고, 벡터화를 통한 빠른 계산속도를 잃는다는 단점이 있다.
적당한 mini-batch size를 찾아 Mini-Batch gradient descent를 수행하는 것이 계산 속도를 높일 수 있다.
적당한 mini-batch size를 찾는 방법은 다음과 같다.
- training set이 작다면, Batch gradient descent를 사용하라. (ex. m ≤ 2,000)
- mini-batch size는 2의 지수값으로 설정하라. (ex. 64, 126, 256, 512)
- mini-batch \(X^{\{t\}}, Y^{\{t\}}\)가 CPU/GPU 메모리에 들어갈 수 있도록 설정하라.
2. Momentum / RMSprop / Adam
Momentum, RMSprop, Adam에 사용되는 개념인 Exponentially weighted average를 알아보자.
1년간 런던 날씨를 수집하여 차트로 나타내면 아래와 같이 분포되어 있다.
이전 날씨 값의 가중 평균을 더하여, 런던 날씨의 trend를 알 수 있다.
Exponentially weighted average 식은 아래와 같다.
\(v_t = \beta v_{t-1} + (1-\beta) \theta_t\)
\(beta\)가 0.9인 경우 \(v\)를 전개하면, 예전 값일수록 가중치가 기하급수적으로 줄어든다.
\(v_{100} = 0.1\theta_{100} + 0.1*(0.9) \theta_{99} + 0.1*(0.9)^2 \theta_{98} + \dots + 0.1*(0.9)^{99} \theta_1\)
예전 날씨는 기하급수적으로 적게 반영되어, \(v_t\)는 약 \(\frac{1}{1-\beta}\) 일 평균 기온으로 볼 수 있다.
Exponentially weighted average의 초반부는 \(v_0=0\)으로 실제 값보다 작은 값을 가지는 경향이 있다.
Bias correction으로 초반부의 값을 더 정확하게 계산할 수 있다.
\(v_t = \beta v_{t-1} + (1-\beta) \theta_t\)
\(v_t = \frac{v_t}{1-\beta^t}\)
2.1 Momentum
Momentum은 Gradient Descent에 Exponentially weighted average를 적용한 알고리즘이다.
Mini-Batch Gradient Descent의 Cost 최적화 과정에 있는 진동폭을 Momentum 사용하여 줄일 수 있다.
\(v_{dW} = \beta v_{dW} + (1-\beta) dW\)
\(v_{db} = \beta v_{db} + (1-\beta) db\)
\(W = W - \alpha v_{dW}\)
\(b = b - \alpha v_{db}\)
2.2 RMSprop
RMSprop는 root mean square propagation의 약자로 제곱평균제곱근(root mean square)이 작은 방향으로 업데이트한다.
(rms가 크면 진동폭이 크고, rms가 작으면 진동폭이 작음을 의미하기 때문에 진동폭이 작은 방향으로 업데이트하여 cost 최적화 속도를 높일 수 있다.)
\(s_{dW} = \beta_2 s_{dW} + (1-\beta_2) dW^2\)
\(s_{db} = \beta_2 s_{db} + (1-\beta_2) db^2\)
\(W = W - \alpha \frac{dW}{\sqrt{s_{dW}}+\epsilon}\)
\(b = b - \alpha \frac{db}{\sqrt{s_{db}}+\epsilon}\)
2.3 Adam
Adam은 Momentum과 RMSprop를 결합한 알고리즘이다.
\(\beta_1\)은 0.9, \(\beta_2\)는 0.999, \(\epsilon\)은 \(10^{-8}\) 값을 권장한다.
\(v_{dW} = \beta_1 v_{dW} + (1-\beta_1) dW\), \(v_{db} = \beta_1 v_{db} + (1-\beta_1) db\) ← Momentum
\(s_{dW} = \beta_2 s_{dW} + (1-\beta_2) dW^2\), \(s_{db} = \beta_2 s_{db} + (1-\beta_2) db^2\) ← RMSproop
\(v_{dW}^{corrected} = \frac{v_{dW}}{1-\beta_1^t}\), \(v_{db}^{corrected} = \frac{v_{db}}{1-\beta_1^t}\), \(s_{dW}^{corrected} = \frac{s_{dW}}{1-\beta_2^t}\), \(s_{db}^{corrected} = \frac{s_{db}}{1-\beta_2^t}\) ← Bias correction
\(W = W - \alpha \frac{v_{dW}^{corrected}}{\sqrt{s_{dW}^{corrected}}+\epsilon}\), \(b = b - \alpha \frac{v_{db}^{corrected}}{\sqrt{s_{db}^{corrected}}+\epsilon}\) ← Adam
3. Learning rate decay
Mini-Batch Gradient Descent의 경우 최적값 주변을 맴돌면서 수렴하지 않을 수 있다.
Learning rate \(\alpha\) 값을 epoch을 진행할수록 감소시켜서 최적값에 수렴시킬 수 있다.
\(\alpha = \frac{1}{1 + decayRate \times epochNum}\alpha_0\)
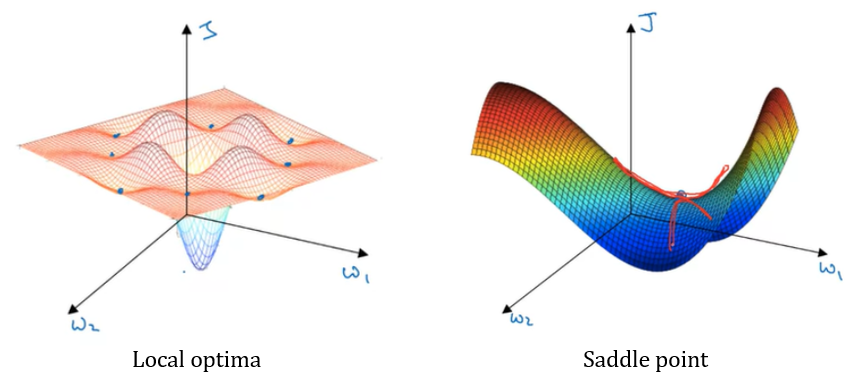
최적화 알고리즘을 사용하다 보면 local optima에 수렴할 것 같지만, 실제 Neural Network에서 local optima에 수렴할 확률은 매우 낮다. 기울기가 0인 지점은 대부분 saddle point이다.
'Deep Learning' 카테고리의 다른 글
| 2.3 Hyperparameter Tuning, Batch Normalization (0) | 2023.03.27 |
|---|---|
| 2.1 Practical Aspects of Deep Learning (0) | 2023.02.28 |
| 1.3 Deep Neural Networks (0) | 2023.02.21 |
| 1.2 Shallow Neural Networks (0) | 2023.02.14 |
| 1.1 Neural Networks Basics (1) | 2023.02.07 |
댓글