Hyperparameter Tuning
신경망을 변경하려면 다양한 hyperparameter를 설정해야 한다. 최적의 hyperparameter 세팅 방법은 무엇일까?
\(\alpha\), \(\beta\), \(\beta_1\), \(\beta_2\), \(\epsilon\), #layers, #hidden units, learning rate decay, mini-batch size 등 신경써야하는 다양한 hyperparameter가 있다.
hyperparameter 검색하는 핵심은 적합한 scale에서 random sampling으로하는 것이다.
Learning rate \(\alpha\), Exponentially weighted averages \(\beta\)의 경우 linear scale이 아닌 log scale에서 탐색하는 것이 효과적이다.
\(\alpha=0.0001, ..., 1\) → \(\alpha=10^{\text{-4*np.random.rand()}}\)
\(\beta=0.9, ..., 0.999\) → \(\beta=1-10^{\text{-1-2*np.random.rand()}}\)
최적의 hyperparameter를 찾았더라도 알고리즘을 개발하면서, 데이터가 변경되면서 다시 hyperparameter를 탐색해야 할 수 있다. hyperparameter를 재탐색하는 방법으로는 1) 한 모델을 돌보는 Babysitting one model과 2) 여러 모델을 훈련하는 Training many models in parallel이 있다. 충분히 많은 컴퓨터가 있으면 Training many models in parallel 방법을 사용하면 된다.

Batch Normalization
layer 별로 입력 데이터의 분포가 달라지는 것을 내부 공변량 변화(Internal Covaraiate Shift)라고 한다.
따라서 hidden layer의 입력 데이터를 정규화하는 과정이 들어가는데, 이것이 Batch Normalization이다.
(실제로는 이전 layer의 \(a\)가 아닌 \(z\)를 정규화한다.)
\(\begin{aligned} & \mu=\frac{1}{m} \sum_i z^{(i)} \\ & \sigma^2=\frac{1}{m} \sum_i\left(z^{(i)}-\mu\right)^2 \\ & z_{\text {norm }}^{(i)}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^2+\epsilon}} \\ & \tilde{z}^{(i)}=\gamma z_{\text {norm }}^{(i)}+\beta\end{aligned}\)
정규화된 \(\tilde{z}\)를 사용하여 학습 속도를 증가시킬 수 있고, 데이터의 분포가 변하는 공변량 변화 문제를 해결할 수 있다. \(\gamma, \beta\)는 모델의 학습가능한 parameter로 적절한 \(\tilde{z}\)값을 가지도록 한다.
Batch Normalization을 Mini-Batch에 사용하면 배치 \(X^{\{t\}}\)마다 아래와 같이 parameter update 한다.
(정규화하면서 parameter \(b\)는 계산에서 제외됨)
\(\begin{gathered}W^{[l]}:=W^{[l]}-\alpha d W^{[l]} \\ \beta^{[l]}:=\beta^{[l]}-\alpha d \beta^{[l]} \\ \gamma^{[l]}:=\gamma^{[l]}-\alpha d \gamma^{[l]}\end{gathered}\)
Tensorflow에서는 tf.nn.batch_normalization 사용으로 간단하게 구현할 수 있다.
Multi-class Classification
지금까지 label이 0 또는 1인 Binary Classification를 다뤄왔다. 이번엔 label이 여러 개인 Multi-class Classification을 알아보자. 예를 들어 이미지의 동물이 고양이/ 강아지/ 병아리인지 분류하는 것이다. 고양이는 class 1, 강아지는 class 2, 병아리는 class 3, 그 외의 이미지는 class 0으로 하자.

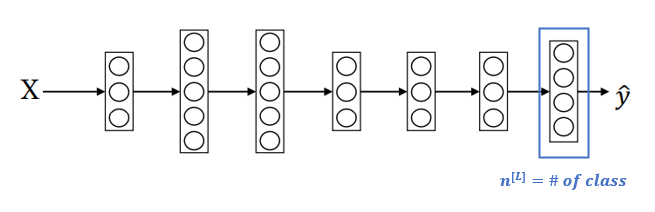
Multi-class Classification의 마지막 layer는 class 수만큼의 노드를 가지고, 각 노드는 class일 확률을 나타낸다. 마지막 layer에서 사용하는 활성화 함수는 Softmax이다. Softmax의 수식은 아래와 같다.
\(\begin{aligned} & \mathrm{t}=e^{\left(z^{[L]}\right)} \\ & a^{[L]}=\frac{e^{z[L]}}{\sum_{i-1}^4 t_i}, a_i^{[L]}=\frac{t_i}{\sum_{i-1}^4 t_i}\end{aligned}\)
아래는 \(z^{[L]}\)이 주어질 때, Softmax를 적용한 예시이다. 예시는 class 0일 확률이 0.842으로 가장 높다.

Multi-calss Classification에서 주로 사용하는 Loss Function은 다음과 같다.
\(\mathscr{L}(\hat{y}, y)=-\sum_{j=1}^c y_j \log \hat{y}_j\)
\(y_k=1\) 이고 나머지 \(y_j\) 값이 0이라면, 정답인 \(\hat {y}_k=1\) 만 남아 Loss가 아래와 같이 계산될 것이다.
\(\mathscr{L}(\hat{y}, y)=-\log \hat{y}_k\)
전체 training set에 대한 Cost는 Loss의 평균으로 구할 수 있다.
\(J\left(W^{[1]}, b^{[1]}, \cdots\right)=\frac{1}{m} \sum_{i=1}^m \mathscr{L}\left(\hat{y}^{(i)}, y^{(i)}\right)\)
'Deep Learning' 카테고리의 다른 글
| 2.2 Optimization Algorithms (0) | 2023.03.14 |
|---|---|
| 2.1 Practical Aspects of Deep Learning (0) | 2023.02.28 |
| 1.3 Deep Neural Networks (0) | 2023.02.21 |
| 1.2 Shallow Neural Networks (0) | 2023.02.14 |
| 1.1 Neural Networks Basics (1) | 2023.02.07 |




댓글